复合奇异环的拓扑动力学及其对应关系

       中山大学物理与天文学院量子工程与精密测量团队邓元刚教授研究组在超冷原子光晶格中针对新奇拓扑物态的研究取得了重要进展。团队发现了复合奇异环结构，揭示了其在准静态和动态环绕过程中的独特行为，并成功建立了这些新奇动力学与拓扑不变量之间的直接联系。此外，团队还提出了基于冷原子系统的可行实验方案，为后续的实验研究提供了重要依据。该研究成果以Topological dynamics and correspondences in composite exceptional rings为题于2025年2月12日发表在国际知名期刊Communications Physics。中山大学物理与天文学院2021级博士生雷周涛为第一作者，邓元刚教授为唯一通讯作者。上述工作得到了国家自然科学基金项目的支持。

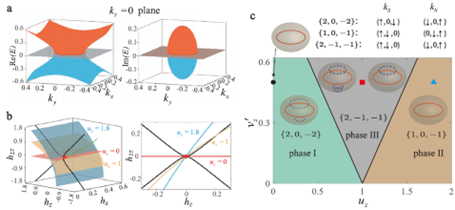
图1：复合奇异环的演化及相应陈数。a kz=0平面的典型能谱。b hx-hz-h2z空间的奇异纽结结构。c 根据陈数划分的复合奇异环的三个拓扑相。红色实线圆表示三阶奇异环，蓝色虚线圆表示外尔奇异环。

        在拓扑物理领域，探索非常规量子相并明确拓扑不变量与特殊物理性质之间的对应关系，一直是该领域的核心研究问题。奇异点作为非厄米系统中特有的简并点，展现出独特的能谱拓扑结构，在量子计算、量子传感等领域展现出巨大的应用潜力。从理论角度看，奇异点的存在使得非厄米系统的能谱拓扑与传统厄米系统截然不同，这种特性为新型量子态的构建和量子算法的设计提供了可能，激发了理论物理学家对其内在规律的深入研究。然而，目前对于高阶和多奇异点体系的研究仍显不足，特别是在复杂的多奇异点系统中，奇异点间的相互作用机制非常复杂，现有理论模型难以准确描述，导致对整体系统拓扑性质的理解受到限制。此外，实验上构建和测量这些复杂体系也面临巨大挑战。 

        在本项研究中，团队通过对非厄米多带哈密顿量及其对称性的深入分析，发现了复合奇异环的存在。该复合奇异环由一个三阶奇异环和多个外尔奇异环组成，展现出由量子化陈数表征的拓扑荷，并通过自旋-向量-动量耦合和自旋-张量-动量耦合实现了对其拓扑特性的有效调控，如图1所示。

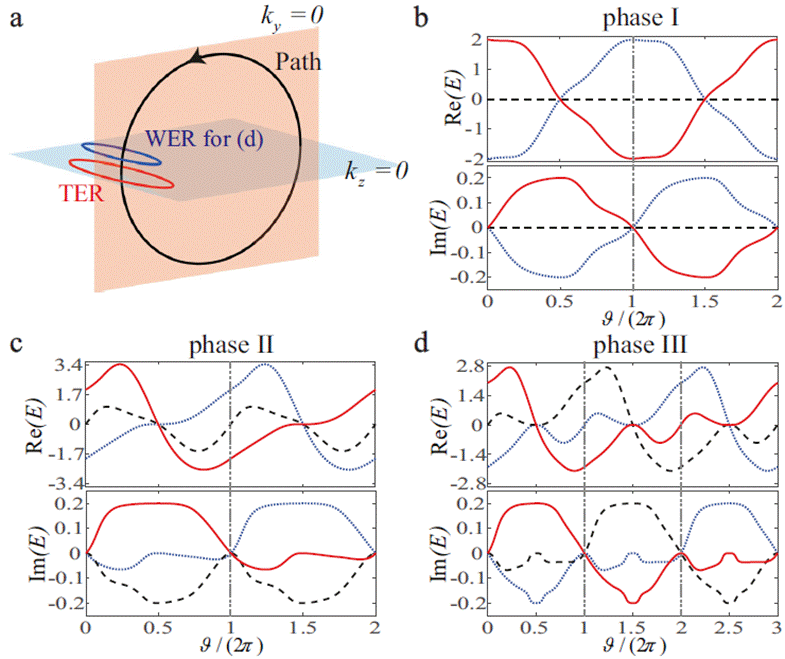
图2：复合奇异环准静态环绕过程中的能谱交换a：环绕复合奇异环的典型闭合路径。b - d：不同参数设置下，复合奇异环准静态环绕过程的能谱响应。 

       奇异点通常表现出非平庸的环绕现象，而复合奇异环展现出的丰富可调拓扑性质带来了更为新奇的物理现象。研究发现，在复合奇异环的准静态环绕过程中，能带编织与非平凡陈数相关，拓扑非平凡（平凡）中间能带对应三重（双重）周期能谱，如图2所示。同时，陈数在动态环绕过程中发挥着至关重要的作用，能够有效预测模式转移。在动态环绕过程中，系统展现出复杂的动力学特性，期望能量随环绕方向和耗散的变化展现出显著的不同，这些行为与非厄米两能带体系相比存在明显差异，如图3所示。这些模式转移与复合奇异环的拓扑荷之间存在直接对应关系，为理解非厄米系统中的动态过程提供了新的视角。

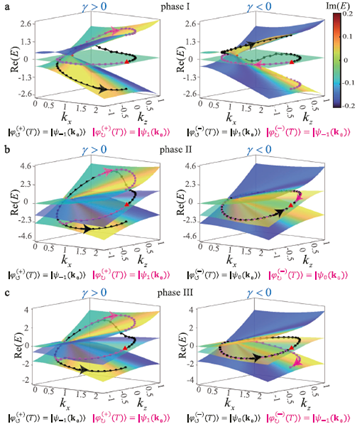
图3：不同方向和耗散下复合奇异环的动态环绕。逆时针（顺时针）环绕过程中的期望能量变化分别用黑色线加圆圈（品红线加方块）表示，初始态能量用红色三角标记。